top of page
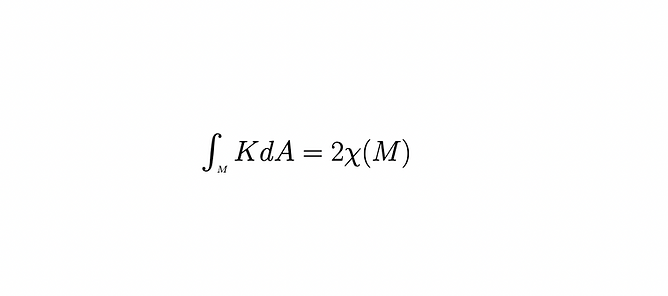
A surface's average Gaussian curvature does not change under a diffeomorphism.
Linking the worlds of differential geometry and topology.
ABOUT THE THEOREM
The Gauss-Bonnet Theorem lies at the intersection of topology and differential geometry. The left hand side of the theorem above displays that global curvature of a surface, a topic in differential geometry, in relation to its Euler characteristic, a notion from topology.
TOPICS COVERED
This website introduces the proof of Gauss-Bonnet Theorem, including the topics needed to understand each step of the proof as well as areas of science it directly is applied to.
bottom of page



